선형 프로그래밍(Linear Programming, LP)은 주어진 선형 관계식의 제약 조건 하에 선형 목적 함수를 최대화하거나 최소화하는 최적의 해를 찾는 방법을 말합니다. 이는 자원 할당, 생산 계획, 교통 네트워크 설계 등 다양한 분야에서 응용됩니다. Kotlin 언어를 활용하여 선형 프로그래밍 문제를 해결하는 방법에 대해 살펴보겠습니다. 본 글에서는 Kotlin을 이용한 선형 프로그래밍의 기본적인 개념 설명과 함께, 간단한 예제를 통해 구현 방법을 소개합니다.
선형 프로그래밍의 기본 개념
선형 프로그래밍 문제는 다음과 같은 형태로 표현됩니다:
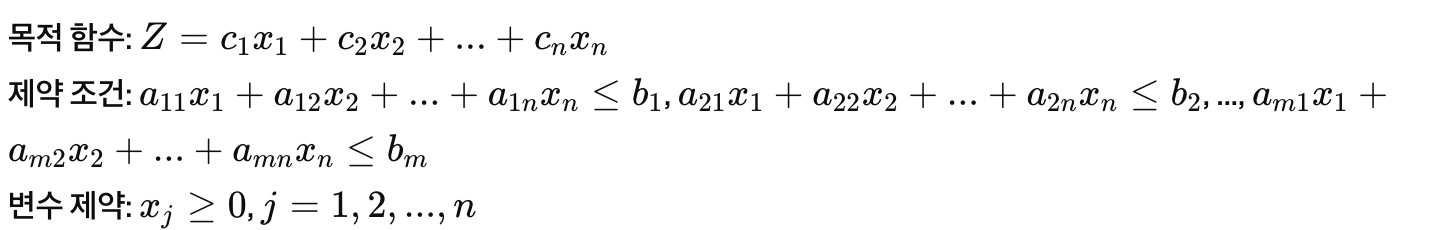
여기서 목적 함수 를 최대화하거나 최소화하는 변수의 값을 찾는 것이 목표입니다.
Kotlin에서의 선형 프로그래밍 구현
Kotlin 자체에는 선형 프로그래밍 문제를 직접 해결할 수 있는 라이브러리가 포함되어 있지 않습니다. 그러나 Kotlin은 Java와 완벽하게 호환되므로, Java용 선형 프로그래밍 라이브러리인 Apache Commons Math와 같은 라이브러리를 사용할 수 있습니다. 예를 들어, 아래는 Apache Commons Math를 사용하여 선형 프로그래밍 문제를 해결하는 간단한 예제입니다.
import org.apache.commons.math3.optim.linear.*
import org.apache.commons.math3.optim.nonlinear.scalar.GoalType
fun solveLinearProblem() {
val constraints = arrayListOf(
LinearConstraint(doubleArrayOf(2.0, 1.0), Relationship.LEQ, 6.0),
LinearConstraint(doubleArrayOf(1.0, 1.0), Relationship.LEQ, 4.0),
LinearConstraint(doubleArrayOf(0.0, 1.0), Relationship.LEQ, 2.0)
)
val objective = LinearObjectiveFunction(doubleArrayOf(5.0, 4.0), 0.0)
val solver = SimplexSolver()
val solution = solver.optimize(objective, LinearConstraintSet(constraints), GoalType.MAXIMIZE, NonNegativeConstraint(true))
println("Solution: Z = ${solution.value}")
for (i in solution.point.indices) {
println("x${i + 1} = ${solution.point[i]}")
}
}
fun main() {
solveLinearProblem()
}
이 예제에서는 두 변수에 대한 선형 목적 함수를 최대화하는 문제를 해결하고 있습니다. 제약 조건은 LinearConstraint 객체로 표현되며, 목적 함수는 LinearObjectiveFunction 객체로 정의됩니다. SimplexSolver 클래스는 이러한 문제를 해결하기 위한 심플렉스 알고리즘을 구현합니다.
결론
선형 프로그래밍은 복잡한 최적화 문제를 해결하는 데 유용한 도구입니다. Kotlin과 Java 라이브러리의 결합을 통해, 개발자는 효율적인 방식으로 이러한 문제에 접근할 수 있습니다. Apache Commons Math와 같은 강력한 라이브러리를 활용함으로써, Kotlin에서도 선형 프로그래밍 문제를 쉽게 해결할 수 있습니다. 이를 통해 개발자는 다양한 최적화 문제를 효과적으로 해결할 수 있는 능력을 갖출 수 있습니다.
'Kotlin' 카테고리의 다른 글
| Kotlin에서 병렬 알고리즘 구현하기: 효율적인 데이터 처리를 위한 접근법 (52) | 2024.04.17 |
|---|---|
| Kotlin을 활용한 상태 공간 탐색: 문제 해결의 체계적 접근 (53) | 2024.04.17 |
| Kotlin을 이용한 NP-완전 문제 해결 방법 탐구 (56) | 2024.04.16 |
| Kotlin에서 그래프 탐색 알고리즘 구현하기: DFS와 BFS (52) | 2024.04.16 |
| Kotlin을 활용한 비트 조작 알고리즘: 기초부터 심화까지 (50) | 2024.04.15 |